저명한 수학자 가우스는 10살 무렵 학교에서 1부터 100까지 더하라는 문제를 받았고, 또래 아이들이 1부터 하나씩 더해갈 때 가우스는 특정한 위치의 숫자들의 합이 101로 일정하다는 것을 알았고 ${(1, 100), (2, 99) …}$ 이들의 개수를 곱함으로써 빠르게 1부터 100까지의 합을 구했습니다. 이런 아이디어는 등차 수열의 합 공식 \(\sum_{i=1}^{n} i = \frac{n(n+1)}{2}\)의 초석이 됩니다. 이 이야기를 떠올리며, 컴퓨터 알고리즘에도 이런 아이디어를 적용할 수 있지 않을까? 하는 호기심이 이 포스트의 출발점입니다.
💡 이 포스트는 Big-O 표기법과 알고리즘 및 점화식에 대한 내용이 포함됩니다.
점화식으로 계산을 줄이는 방법?
이 아이디어의 시작은 고등학교때 배웠던 수열과 점화식에 있습니다.
만약 어떤 문제를 풀다가 우연히 $a_{n+1} = 2a_n+3$ 이런 점화식 관계를 발견했다고 가정해봅시다.
이런 점화식의 수열은 초항이 $1$이라 가정했을때 $1, 5, 13, 29…$이런식으로 형성될 것입니다.
$a_{10}$을 구하려면 $a_{1}$,$a_{2}$..$a_{9}$ 이렇게 순차적으로 구해나가야하기 때문에 계산을 10번 반복해야합니다.
하지만 고등학교에 $a_{n+1} = pa_n+q$ 형태의 점화식 일반항을 구해본 기억이 있을 것 입니다.
\[a_{n+1} = p a_n + q \quad (n \geq 1)\]\(a_n\)을 알파로 치환합니다. 미정계수법 참고
\[\alpha = p \alpha + q \\,\\\ \alpha = \frac{q}{1 - p} \quad (p \neq 1)\]\(a_n-\alpha\) 꼴의 등비 수열로 만들어줍니다. 자세한 계산을 생략하였습니다.
\[a_{n+1} - \alpha = p (a_n - \alpha) \quad \\\]등비수열의 일반항 공식을 적용해줍니다.
\[a_n - \alpha = (a_1 - \alpha) p^{n-1} \\ a_n = \alpha + (a_1 - \alpha) p^{n-1} \\\]미정계수법을 통해 점화식의 모양을 적절히 바꿔줌으로써 우리에게 편한 등비수열 꼴로 변환시켰고
널리 알려진 등비수열 공식을 통해 일반항을 도출할 수 있었습니다.
이제 위의 예시 $a_{n+1} = 2a_n+3$ 에 적용시키면 일반항은 $a_{n} = 4*2^{n-1}-3$ 가 됩니다.
$a_1 = 1, \ a_2=5, \ a_3=13…$ 대입해보면 올바른 식을 도출했음을 알 수 있습니다.
이 식을 통해 여러번 계산하는 대신 한번의 계산으로 답을 도출할 수 있습니다.
피보나치를 통한 예시
이제 이런 아이디어를 수학과 컴퓨터과학의 대표적인 수열 중 하나인 피보나치 수열의 n번째 항을 구해보겠습니다.
피보나치 수열의 점화식은 다음과 같습니다.
\begin{equation} F_0 = 0, \quad F_1 = 1 \end{equation}
\begin{equation} F_{n+2} = F_{n+1} + F_{n} \quad \text{for} \quad n \geq 0 \end{equation}
직관적이고 기본적인 재귀를 활용한 방식
우선 가장 기본적인 피보나치 수열의 n번째 항을 구하는 알고리즘을 작성해보면,
def fibonacci_basic(n):
if n <= 1:
return n
return fibonacci_basic(n-1) + fibonacci_basic(n-2)
이렇게 작성할 수 있고 이 알고리즘은 다음과 같이 자라나는 계산 프로세스를 만들어냅니다.
이런 계산 프로세스의 시간복잡도는 $O(2^n)$입니다.
기본적으로 모든 단계에서 두갈래로 자라나기 때문에 $O(2^n)$에 가깝지만 한 갈래는 나머지 갈래보다 한 차수 낮은 계산을 하기 때문에 피보나치의 수열의 시간복잡도는 일반적으로$O(\phi^n)$의 시간복잡도를 가집니다.
엄밀히 말하면 $O(\phi^n)$ = $O\left(\left(\frac{1 + \sqrt{5}}{2}\right)^n\right)$ 이지만 이번 포스트에선 $O(2^n)$로 편의상 근사하겠습니다.
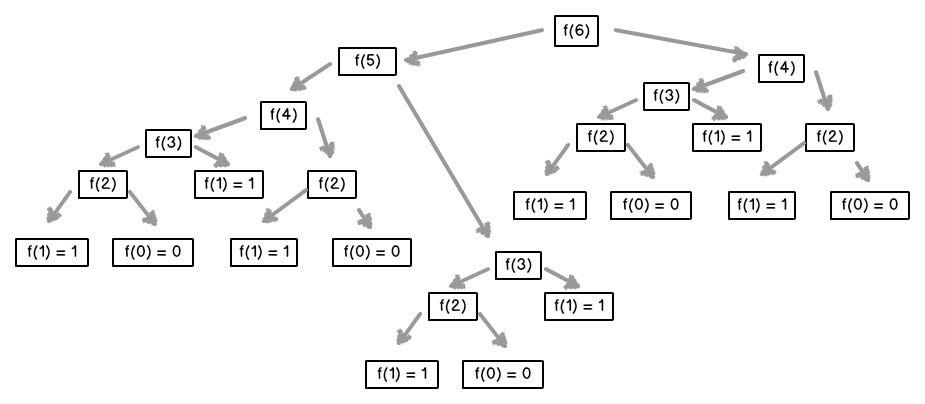
위의 기본 재귀 알고리즘(fibonacci_basic)에서는 동일한 하위 문제(예: $f(3)$)를 여러 번 계산하는 비효율이 발생합니다.
예를 들어, $f(5)$를 구하려면 $f(4)$와 $f(3)$을 계산하고, $f(4)$를 구할 때 다시 $f(3)$과 $f(2)$를 계산하는 식으로 중복이 반복됩니다.
이로 인해 시간 복잡도가 $O(2^n)$에 달하며, $n$이 커질수록 계산량이 기하급수적으로 증가합니다.
이전 계산을 활용하기
이 문제를 해결하기 위해 Dynamic Programming(기억하며 풀기)을 적용할 수 있습니다.
기억하며 풀기는 이전에 계산한 결과를 저장해두고, 필요할 때 재사용함으로써 중복 계산을 피하는 기법입니다.
이를 구현한 코드가 바로 아래와 같은 메모이제이션(Memoization) 방식입니다:
def fibonacci_memo(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
return memo[n]
위와 같은 코드에선 한 갈래의 계산을 이전 계산에서 했고 그 값을 사용하기 때문에 한 갈래로만 뻗어나가게 됩니다.
따라서 시간복잡도는 $O(n)$ 가 됩니다.
본격적으로 사람의 시간으로 컴퓨터의 시간 아껴보기
수학을 조금 활용하면 좀 더 최적화가 가능합니다 .
기억하며 풀기 방식으로 시간 복잡도를 $O(n)$까지 줄였지만,
수학적 패턴을 활용하면 피보나치 수열의 $n$번째 항을 훨씬 더 빠르게 구할 수 있습니다.
이 방식은 점화식의 반복 적용을 분할 정복으로 최적화한 것으로, 아래 코드를 통해 구현됩니다.
def fib(n):
return fib_iter(1, 0, 0, 1, n)
def fib_iter(a, b, p, q, count):
if count == 0:
return b
elif count % 2 == 0:
p_prime = p**2 + q**2
q_prime = q**2 + 2*p*q
return fib_iter(a, b, p_prime, q_prime, count // 2)
else:
a_prime = b*q + a*q + a*p
b_prime = b*p + a*q
return fib_iter(a_prime, b_prime, p, q, count - 1)
⚠️ 여기서부터는 수식 정리 내용이 많습니다. 스킵 하셔도 무방합니다.
이 알고리즘은 피보나치 수열의 연속된 두 항 $a$와 $b$를 특정 연산(여기서 T 연산이라 부르겠습니다)을 통해 변환하면서 $n$번째 항을 계산합니다.
T 연산은 다음과 같이 정의됩니다.
초기값 $a_1, b_1$이 주어졌을 때:
$a_2 = b_1 q + a_1 q + a_1 p$
$b_2 = b_1 p + a_1 q$
여기서 $p$와 $q$는 변환에 사용되는 계수로, 피보나치 수열의 경우 초기값은 $p=0$, $q=1$로 시작합니다.
이 연산을 반복 적용하면 다음 항들이 계산됩니다.
T 연산을 한 번 더 적용해 $a_3, b_3$을 구해보겠습니다 (작성 편의를 위해 $a_1 = a$, $b_1 = b$로 표기):
$a_2 = b q + a q + a p$
$b_2 = b p + a q$
이제 $a_2, b_2$에 다시 T 연산을 적용하면:
$a_3 = b_2 q + a_2 q + a_2 p$
$= (b p + a q) q + (b q + a q + a p) q + (b q + a q + a p) p$ $= b (q^2 + 2pq) + a (p^2 + q^2 + q^2 + 2pq)$
$b_3 = b_2 p + a_2 q$
$= (b p + a q) p + (b q + a q + a p) q$ $= b (p^2 + q^2) + a (2pq + q^2)$
여기서 새로운 계수를 정의합니다:
$p’ = p^2 + q^2$
$q’ = q^2 + 2pq$
그러면:
$a_3 = b q’ + a q’ + a p’$
$b_3 = b p’ + a q’$
놀랍게도, $a_3, b_3$는 $p$와 $q$를 $p’, q’$로 바꾼 T 연산과 동일한 형태를 가집니다.
즉, T 연산을 두 번 적용한 효과를 한 번의 계산으로 줄일 수 있습니다!
이 패턴을 활용하면, $n$이 짝수일 때마다 $p$와 $q$를 $p’, q’$로 갱신하고 반복 횟수를 절반으로 줄일 수 있습니다.
$n$이 홀수일 때는 T 연산을 한 번 적용 ($a’ = b q + a q + a p$, $b’ = b p + a q$).
$n$이 짝수일 때는 $p’ = p^2 + q^2$, $q’ = q^2 + 2pq$로 갱신 후 $n/2$로 진행.
이를 코드로 구현한 것이 fib_iter입니다.
초기값 $a=1$, $b=0$, $p=0$, $q=1$에서 시작해 $n$번의 변환을 거치면 $F_n$을 구할 수 있습니다.
이런 접근을 통해 $O(\log n)$의 시간 복잡도를 얻을 수 있습니다.
단 한번의 계산으로 끝내는 방법: 점화식 -> 일반항
피보나치 수열의 $n$번째 항을 $O(\log n)$으로 계산하는 방법도 훌륭하지만, 수학적으로 점화식을 일반항으로 풀어내면 단 한 번의 계산으로 $F_n$을 구할 수 있습니다. 이를 위해 특성방정식을 활용한 방법을 사용하겠습니다.
간단한 예시로 시작
본격적으로 피보나치 수열의 일반항을 구하기 전에, 비슷한 형태의 점화식 $a_{n+2} - a_{n+1} - 2a_n = 0$을 풀어보겠습니다.
-
특성방정식을 구합니다:
주어진 점화식 $a_{n+2} - a_{n+1} - 2a_n = 0$에서, 특성방정식을 세웁니다: $r^2 - r - 2 = 0$ -
인수분해하여 근을 구합니다:
$r^2 - r - 2 = (r-2)(r+1) = 0$ 따라서 근은 $r_1 = 2$, $r_2 = -1$입니다. -
두 근을 정의합니다:
$\alpha = 2$, $\beta = -1$라 하고, 이들의 관계를 확인하면: $\alpha + \beta = 2 + (-1) = 1$ $\alpha \cdot \beta = 2 \cdot (-1) = -2$ -
일반항을 구하기 위해 점화식을 변형합니다:
$a_{n+2} - \alpha a_{n+1} = \beta (a_{n+1} - \alpha a_n)$ … (1)
$a_{n+2} - \beta a_{n+1} = \alpha (a_{n+1} - \beta a_n)$ … (2) -
새로운 수열을 정의합니다:
식 (1)에서 $b_n = a_{n+1} - \alpha a_n$이라 정의하면:
$b_{n+1} = a_{n+2} - \alpha a_{n+1} = \beta b_n$.
즉, $b_{n+1} = \beta b_n$이므로 $b_n = b_1 \cdot \beta^{n-1}$입니다.
여기서 $b_1 = a_2 - \alpha a_1$입니다.마찬가지로 식 (2)에서 $c_n = a_{n+1} - \beta a_n$이라 정의하면:
$c_{n+1} = a_{n+2} - \beta a_{n+1} = \alpha c_n$
즉, $c_{n+1} = \alpha c_n$이므로 $c_n = c_1 \cdot \alpha^{n-1}$입니다.
여기서 $c_1 = a_2 - \beta a_1$입니다. -
$a_n$을 구합니다:
$b_n = a_{n+1} - \alpha a_n$이므로 $a_{n+1} = b_n + \alpha a_n$ … (3)
$c_n = a_{n+1} - \beta a_n$이므로 $a_{n+1} = c_n + \beta a_n$ … (4)식 (3)과 (4)가 같으므로:
$b_n + \alpha a_n = c_n + \beta a_n$
$b_n - c_n = (\beta - \alpha) a_n$
$a_n = \frac{b_n - c_n}{\beta - \alpha} = \frac{c_n - b_n}{\alpha - \beta}$ -
$b_n$과 $c_n$을 대입합니다:
$b_n = b_1 \cdot \beta^{n-1}$, $c_n = c_1 \cdot \alpha^{n-1}$을 대입하면:
$a_n = \frac{c_1 \cdot \alpha^{n-1} - b_1 \cdot \beta^{n-1}}{\alpha - \beta}$ -
구체적인 값을 넣습니다:
$\alpha = 2$, $\beta = -1$, $\alpha - \beta = 2 - (-1) = 3$을 대입하면:
$a_n = \frac{c_1 \cdot 2^{n-1} - b_1 \cdot (-1)^{n-1}}{3}$
여기서 $c_1$과 $b_1$은 초기 조건($a_1$, $a_2$)에 따라 결정됩니다.
이렇게 특성방정식의 근을 통해 점화식의 일반항을 도출했습니다. 이 예시는 두 근이 정수인 경우였습니다.
피보나치 수열의 일반항 구하기
이제 피보나치 수열 $F_{n+2} = F_{n+1} + F_n$ ($F_0 = 0$, $F_1 = 1$)의 일반항을 구해보겠습니다.
-
특성방정식을 구합니다:
$r^2 - r - 1 = 0$ -
근을 구합니다:
$r = \frac{1 \pm \sqrt{1 + 4}}{2} = \frac{1 \pm \sqrt{5}}{2}$
따라서:
$\alpha = \frac{1 + \sqrt{5}}{2}$ (황금비, $\phi$), $\beta = \frac{1 - \sqrt{5}}{2}$
관계를 확인하면:
$\alpha + \beta = 1$, $\alpha \beta = -1$, $\alpha > \beta$ -
점화식을 변형합니다:
$a_{n+2} - a_{n+1} = \alpha (a_{n+1} - a_n)$ … (①)
$a_{n+2} - \beta a_{n+1} = \alpha (a_{n+1} - \beta a_n)$ … (②) -
새로운 수열을 정의합니다:
식 (②)에서 $b_n = a_{n+1} - \alpha a_n$이라 하면 ($b_1 = 1 - \alpha = \beta$):
$b_{n+1} = \beta b_n$
$b_n = a_{n+1} - \alpha a_n = \beta^{n-1}$ … (③)마찬가지로:
$a_{n+1} - \beta a_n = \alpha^{n-1}$ … (④) -
$a_n$을 구합니다:
식 (③) - (④): $(\alpha - \beta) a_n = (\alpha^{n-1} - \beta^{n-1})$ $a_n = \frac{1}{\alpha - \beta} [(\alpha^{n-1} - \beta^{n-1})]$ -
값을 대입합니다:
$\alpha - \beta = \frac{1 + \sqrt{5}}{2} - \frac{1 - \sqrt{5}}{2} = \sqrt{5}$
따라서:
$a_n = \frac{1}{\sqrt{5}} \left[ \left( \frac{1 + \sqrt{5}}{2} \right)^{n-1} - \left( \frac{1 - \sqrt{5}}{2} \right)^{n-1} \right]$
이것이 피보나치 수열의 일반항(Binet 공식)입니다.
초기 조건 $F_0 = 0$, $F_1 = 1$에 맞게 조정하면 $n-1$ 대신 $n$을 사용해:
$F_n = \frac{1}{\sqrt{5}} \left[ \left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n \right]$로 나타낼 수도 있습니다.
비넷 공식을 활용한 알고리즘은 다음과 같이 구현됩니다.
phi = (1 + math.sqrt(5)) / 2
def fibonacci_binet(n):
return round((phi**n - ((-phi)**-n)) / math.sqrt(5))
이 공식은 재귀, DP, 분할 정복 없이도 $F_n$을 단일 계산으로 구할 수 있어 시간 복잡도 $O(1)$을 달성합니다.
단, 컴퓨터에서는 실수 연산의 정밀도와 큰 수의 지수 계산이 문제가 될 수 있습니다.
실제로 n=71 부터 오차가 나타나기 시작하고 n이 커질수록 그 오차는 커집니다.
실제로 더 빨라졌을까요?
직접 위의 코드들로 구현하여 실제 속도를 비교해보겠습니다. (CPU: M4)
#!/usr/bin/env python3
import time
import math
def fibonacci_basic(n):
if n <= 1:
return n
return fibonacci_basic(n-1) + fibonacci_basic(n-2)
def fibonacci_memo(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
return memo[n]
def fibonacci_log(n):
return fib_iter(1, 0, 0, 1, n)
def fib_iter(a, b, p, q, count):
if count == 0:
return b
elif count % 2 == 0:
p_prime = p**2 + q**2
q_prime = q**2 + 2*p*q
return fib_iter(a, b, p_prime, q_prime, count // 2)
else:
a_prime = b*q + a*q + a*p
b_prime = b*p + a*q
return fib_iter(a_prime, b_prime, p, q, count - 1)
phi = (1 + math.sqrt(5)) / 2
def fibonacci_binet(n):
return round((phi**n - ((-phi)**-n)) / math.sqrt(5))
def time_function(func, n):
start = time.perf_counter()
result = func(n)
end = time.perf_counter()
return end - start, result
n_values = [30, 40, 70, 71, 72]
for n in n_values:
time_basic, result_basic = time_function(fibonacci_basic, n)
time_memo, result_memo = time_function(fibonacci_memo, n)
time_log, result_log = time_function(fibonacci_log, n)
time_binet, result_binet = time_function(fibonacci_binet, n)
print(f"n = {n}")
print(f"Recursion {time_basic:.6f} seconds Result:: {result_basic}")
print(f"Memoization {time_memo:.6f} seconds Result: {result_memo}")
print(f"Divide {time_log:.6f} seconds Result: {result_log}")
print(f"Binet {time_binet:.6f} seconds Result: {result_binet}")
print()
n = 40 이상 부터는 기본 재귀를 활용한 방식에서 너무 많은 시간을 소요하므로 주석 처리 후 테스트 하였습니다.
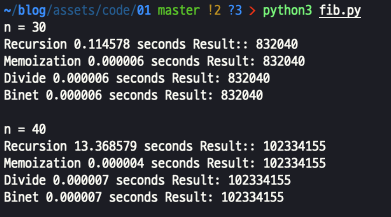
재귀 방식은 40부터 시간이 기하급수적으로 증가하여 10초 이상 소요되는 것을 확인할 수 있습니다.
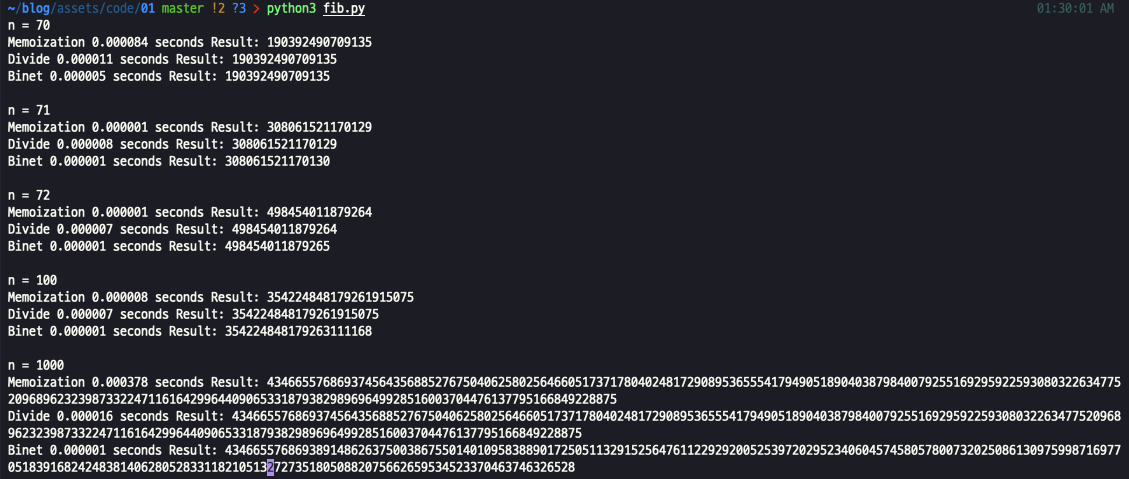
n=71 부터 비넷 공식은 부정확한 답을 내놓는 것을 확인할 수 있고,
n=1000 에서는 각 알고리즘의 시간 차이를 명확하게 확인할 수 있습니다.
결론
사람의 시간을 사용하여 컴퓨터의 시간을 아끼는 방법을 알아보았습니다.
위의 테스트에서도 확인하였듯이 일반적인 경우 O(n)도 상당히 빠른 속도를 보여줍니다.
따라서 일반적인 상황에서 이런 방식을 항상 채택하긴 어렵습니다.
특히 일반항 방식은 실무에서 직접 구현하기 어렵고, 수치적 오차를 고려해야 합니다.
하지만 특정한 상황에서 이런 가능성을 알고 있는 것은 도움이 될 것이라 생각합니다.

